Side-rankering

Google-søgemaskinen er, som de fleste ved, ret berømt, du har måske oven i købet brugt den til at ankomme her – forhåbentlig lå denne post højt på resultatlisten.

Alt det startede med en algoritme ved navnet PageRank, som gjorde det muligt for computere at lave rankeringer af internet-sider og ved et slag lavede internet-søgemaskiner til relevans-maskiner i stedet for store leksikale opslagsværker.

Ideen bag PageRank er ret genial, da man ikke kigger på selve siden, og derved frigiver forfatteren af siden for fristelsen at manipulere med søgemaskinen, men måler i stedet en sides relevans på, hvor mange andre sider der linker til siden. Faktisk kan man forstille sig at hver side på internettet “stemmer” på andre sider. Så hvis en side linker til en anden, så siger man at siden stemmer på den anden side.

Men hov.. tænker den kloge læser sikkert, så kunne forfatteren jo bare lave million sider som linker til siden, så er problemet løst, og man kommer til at stå øverst på alle søgninger alligevel. Men så nemt er det ikke. For PageRank bruger den stemmendes egen pagerank til at beregne stemmens værdi, således at hvis der ikke er nogen som stemmer på den side som stemmer, er stemmerens stemme ikke noget værd. Lad os tage et eksempel:

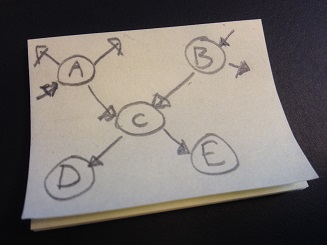
Lad os forestille os at følgende er et udsnit af internettet og lad os beregne PageRank for siden C:

For at beregne dette skal man kigge på alle de sider som peger på C, hvilket er A og B. Antag nu at A’s PageRank er Ra og B’s er Rb.

Da A har “stemt” på tre sider (altså 3 links på siden til andre sider), derfor vil A’s stemme på C give en værdi på Ra/3, Siden B’s stemme derimod tilføjer Rb/2 da siden B kun har stemt på 2 sider. Det betyder at C’s pagerank er:

Rc = Ra/3 + Rb/2

Envidere stemmer siden C på 2 andre sider, derfor tilføjer Siden C, Rc/2 til D og E’s pagerank. Det betyder derfor at nu flere vigtige sider som peger på din side nu højere PageRank får den. Men hvad så med A og B, og de sider som peger på dem? Hvordan starter man? Faktisk starter man med det hele.

Kigger man f.eks. et meget forsimplet internet som kun har 3 sider, så ender man med 3 ligninger med 3 ubekendte og ingen konstanter, hvilket ikke har nogen entydig løsning. Men da kan man tilføje et ekstra krav om at summen af alle Pageranks skal være 1, hvilket er nok til at man kan finde en løsning. Dette kan man løse ved hjælp af Gausisk udelukkelse.

Problemet er nu at det bliver kompliceret hvis man har et faktisk internet. Men heldigvis kan problemet defineres ved hjælp af matricer og eigenvektorer og kan derefter løses det med en iterativ algoritme ved navnet power iteration, som kan være en opgave til læseren at kigge på.

Når man så har fundet PageRank kommer det meget mere komplekse problemer man skal løse hvis man er en søgemaskine: Hvilke sider skal man returnere på hvilke søgninger, og hvordan man laver disse koblinger er normalt en velbevaret hemmelighed.

Men en måde kunne være at man laver det der hedder en tf–idf som beregner vigtigheden af ord i dokumenter. Når der bliver søgt på et ord, returner de dokumenter hvor ordet er mest vigtig sorteret efter pagerank. Men Google gør det helt sikkert noget som er bedre og mere effektivt.